This post is also available in:
 Deutsch
Deutsch
Einfache Modelle helfen bei der Entscheidung
Inspiriert vom Deckungsbeitragsrechner des Preisspezialisten Roman Kmenta zeige ich hier, wie man aus zwei Verkaufspreisen, zwei abgesetzten Mengen, den Fixkosten und den variablen Stückkosten – also den Kosten pro Stück, die nur bei tatsächlicher Produktion anfallen – den Verkaufspreis berechnen kann, der den größten Gewinn erzeugt. Voraussetzung ist natürlich, dass der Unternehmer den Preis überhaupt beeinflussen kann. Dies ist der Normalfall.
Die Berechnung (Cournot-Punkt)
Als Beispiel nehme ich einen vereinfachten Fall aus dem Obst- und Gemüsehandel. Wir haben durch Experimente herausgefunden, dass wir bei 3 € Verkaufspreis je Schale am Tag 300 Packungen Erdbeeren, bei 4 € Verkaufspreis je Schale aber nur 200 Packungen Erdbeeren verkaufen. Ein Euro Preiserhöhung macht also 100 Packungen Unterschied. Die Preis-Absatz-Funktion ist also Verkaufspreis = 6 – 0,01 * abgesetzte_Menge. Der Verkaufsstand kostet uns 200 € pro Tag (Fixkosten), der Plantagenbesitzer liefert uns die Erdbeeren für 2 € je Schale an den Stand (variable Stückkosten der Erdbeeren). Der Gewinn pro Tag ist abgesetzte Menge mal Preis – abgesetzte Menge * variable Stückkosten – Fixkosten. Der Gewinn G soll größtmöglich ausfallen, bei einem Preis von 6 € verkaufen wir aber nichts mehr, wie die Preis-Absatz-Funktion aussagt. Durch Einsetzen ergibt sich folgendes:
Gewinn = Menge * (6 – 0,01 Menge) – Menge * 2 – 200,
umgeformt:
Gewinn = Menge * 6 – 0,01 Menge^2 – Menge * 2 – 200
und weiter:
Gewinn = Menge * 4 – 0,01 Menge^2 – 200
In der Oberstufenmathematik haben wir gelernt, dass die erste Ableitung (Steigung) einer Parabelfunktion am Maximum (des Gewinns) 0 ist. Die Funktion zeigt den Gewinn als Ergebnis von Preis und Menge. Beginnend von einem sehr niedrigen Preis steigt der Gewinn zunächst, wenn wir die Preise erhöhen. Es gibt einen Gewinnmaximum (mögliche Gewinnsteigerung = 0), dann sinkt der Gewinn wieder, wenn wir die Preise weiter erhöhen. Grund dafür sind sinkende Absatzmengen.
Bilden wir die erste Ableitung G´, die wir 0 setzen müssen (keine Steigung des Gewinns mehr):
G´ = 4 – 0,02 Menge
0 = 4 – 0,02 Menge
4 = 0,02 Menge
Menge = 200
setzen wir wieder in die Preis-Absatzfunktion ein, gilt: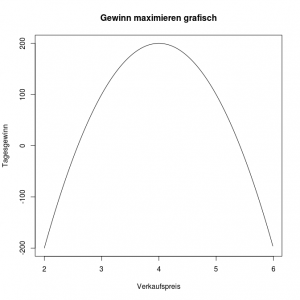 Cournot-Punkt
Cournot-Punkt
Preis = 6 – 0,01 * 200
Preis = 4 (Euro)
Gewinn = 200 € (pro Tag!!!)
Folgen der Cournot-Analyse für den Verkaufspreis
Bei diesem Modell kann man die Einkaufspreise ändern und staunen, wie sich der Verkaufspreis ändert, so wird z. B. bei einer Senkung der Einkaufspreise um 50 ct der gewinnmaximale Verkaufspreis um 50 ct sinken und der Gewinn um 100 € steigen (pro Tag).
Natürlich lässt sich das Modell wegen einschränkender Annahmen nicht direkt in die Realität umsetzen. Aus eigener Erfahrung mit Straßenverkaufsständen für Obst kann ich sagen, dass die Gewinne nicht ganz so hoch liegen wie in diesem Beispiel mit 25%.
Wie gut anwendbar ist das Modell
Das Modell setzt eine bekannte, stabile und möglichst lineare Nachfragefunktion voraus. An genau der scheitert der Einsatz meistens. Ansätze zur Ermittlung finden Sie hier.


Zur Grafik: Man sieht, wie leicht man durch falsch gesetzte Preise in die Verlustzone gerät. Allerdings können die Preise in diesem Modell zwischen 3,50 € und 4,50 € schwanken, ohne dass sich am Gewinn große Änderungen ergeben.